In-Class Slides for Unit 3
Understanding Inventory Changes and Investment
We start with I (investment spending) as it appears in the calculation of GDP = C+I+G+(X-M).
I represents all spending on investment goods. There’s really three sub-types of investment goods: capital equipment & plant for firms, new residential houses just built, and additions to inventory. Of these, the amounts spent on the first two, capital equipment and residential housing are clearly “planned” spending. Firms think about these and plan ahead to spend this much money. The third one, additions to inventory, happens partly by accident. That is, firms don’t always plan to add to inventory or to reduce inventory. Instead inventory changes because firms have to produce things in advance of selling them to consumers and the firms can’t/don’t always forecast that consumer demand very well. When they forecast consumer demand in the future well, then inventory stays unchanged – they produce exactly this month what they end up selling next month and so on.
But when a firm underestimates future consumer demand, it doesn’t produce enough ahead of time. When the consumer demand happens next period, it reduces inventory. We have negative “unplanned investment spending” because the inventory gets reduced.
If a firm overestimates future consumer demand, it produces this period and puts it in inventory. Then next period, customers don’t buy as much as expected and the amount of inventory increases. The firm experiences an unplanned addition to inventory next period – a positive “unplanned investment spending”.
Examples:
No change in inventory:
| period | Production | Sales to Consumers | inventory balance | addition (decrease) in inventory |
| 1 | 100 | 100 | 100 (from previous production) | 0 |
| 2 | 100 | 100 | 100 (add 100 from production and subtract 100 for sales) | 0 |
| 3 | 100 | 100 | 100 (add 100 from production and subtract 100 for sales) | 0 |
Unplanned addition to inventory:
| period | Production | Sales to Consumers | inventory balance | addition (decrease) in inventory |
| 1 | 100 | 100 | 100 (from previous production) | 0 |
| 2 | 100 | 90 | 110 (add 100 from production and subtract 90 for sales) | 10 |
| 3 | 100 | 90 | 120 (add 100 from production and subtract 90 for sales) | 10 |
Unplanned reduction in inventory:
| period | Production | Sales to Consumers | inventory balance | addition (decrease) in inventory |
| 1 | 100 | 100 | 100 (from previous production) | 0 |
| 2 | 100 | 120 | 80 (add 100 from production and subtract 120 for sales) | -20 |
| 3 | 100 | 120 | 60 (add 100 from production and subtract 120 for sales) | -20 |
Now
Nominal and Real Calculations with GDP (including formulas):
This tutorial will show the mathematical relationships between Nominal GDP, Real GDP, and a Price Index.
A. Relationship between Nominal, Real, and Price Index
Like many calculations in economics, what we have is a defined mathematical relationship or equation that has several variables in it. In this case, there are three variables: a nominal GDP amount, a “real” GDP amount, and a value for the price index for that year. The way these three are related is:
Like any such math relationship, if we know two of the variables, we can calculate the third. The reason we are dividing the PriceIndex by 100 is because of how price indexes are typically reported. In general price indexes are reported as an abstract scale where the general level of prices in the economy (think “average price of everything”), is reported as 100.00 in some starting year. The starting year is called the base year. If prices go up, the price index also goes up, but it is always relative to the prices that existed in the base year.
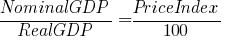
So, for example, if we know NominalGDP and we know the PriceIndex, we can calculate RealGDP. Let’s suppose the NominalGDP in the year 2005 is $6,000 million. (this is a pretty small country). Let’s also suppose the PriceIndex for the year 2005 in this country is 120.00 using a price index for which the base year was 1999. Let’s calculate the RealGDP by rearranging our earlier formula to isolate RealGDP and then we will plug in the values for the two variables we know. We get an answer of $5,000 for RealGDP.
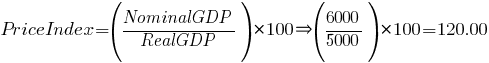
We get an answer of $5,000 for RealGDP. What does this number represent? What does it tell us? Well, it tells us that if quantities of the physical goods and services produced in the year 2005 were sold at the prices that existed back in 1999 (the base year), the total value would have been $5,000. This is RealGDP number for 2005 is also sometimes referred to as representing “2005 GDP at 1999 prices” or as “2005 GDP in 1999 dollars”.
But what if we only knew the RealGDP number and the PriceIndex, but didn’t know nominal GDP? Again, we could rearrange the original formula and plug in the numbers we have and calculate:
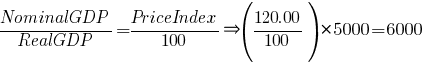
We get a value of $6,000 for NominalGDP. Of course, in real life economists usually already know the nominal amount because it is what can be directly observed by counting people’s actual purchases. Usually we are calculating the RealGDP.
It is possible, of course, that we may know NominalGDP and RealGDP, but the economist who gave you that data didn’t tell you the value for the price index she used. You can calculate it:
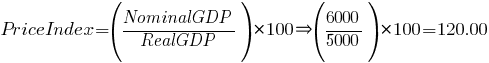
![]()
B. Generalizing the Relationship between “Nominal” and “Real”
As long we are dealing with actual monetary amounts, we can calculate nominal and real values. It doesn’t always have to be GDP. It could be Consumer Spending. Or Total Sales of Homes. Or even the cost of a loaf of bread. As long we have an observed value that is based on a sale price in a particular year, AND we know a relevant price index, we can estimate the “real” value of the item. This is how economists compare the values of things from different years. The relationships and calculations can actually be used to when dealing with any economic variable that has both “nominal” and “real” amounts.
This enables us to take the effects of inflation (money that is losing it’s value) out of the question. Besides being a research issue for economists, it can also help make some fun comparisons. For example, have you ever heard your parents or some other older person talk about how much cheaper things were “back when”? For example, suppose you want to buy a car and you’re looking at a $15,000 new car. You parents (whom you want to help you finance the car), start saying that “when they bought their first care back in 1981, the only paid $8,000. Well, with a little adjustment for inflation by using the price index (in this case the consumer price index), we find that $8,000 in 1981 is the real equivalent of $18,332 in 2007! You’re actually looking at a cheaper car than they did!
If you’re interested there are some websites that help you make this calculation automatically. Two web sites I know of are:
http://146.142.4.24/cgi-bin/cpicalc.pl and http://www.minneapolisfed.org/research/data/us/calc/
![]()
C. Calculating Growth Rates
Generally, the reason we want to know Real GDP is because we are interested in the rate of real growth in the economy – the rate at which we are actually being able to produce more goods and services than before. If the growth rate is a positive percentage number, it means the economy is growing and there are more goods becoming available to support more people and better living standards. If the growth rate is negative.
To calculate a growth rate for the current year, we need the same variable from two different years: the current year and the previous year. Then we calculate as follows:
![delim{[}{(currentYearAmount/previousYearAmount) - 1.00}{]} * 100 = PercentGrowth delim{[}{(currentYearAmount/previousYearAmount) - 1.00}{]} * 100 = PercentGrowth](https://macro.econproph.net/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_956.5_328adad4c379ad6e8efdce5b85bc7ed6.png)
The times by 100 is only necessary to convert the decimal fraction into a true percentage number.
Thus, suppose we have a RealGDP of $5,000 in the year 2004 and $5,334 in the following year, 2005. Then the percentage growth from 2004 to 2005 is:
![delim{[}{(5334/5000) -1 }{]} * 100 = 6.7% delim{[}{(5334/5000) -1 }{]} * 100 = 6.7%](https://macro.econproph.net/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_956.5_f479501d57dea716b82e3cdc0a65bd74.png)
In this case we got a 6.7% Real Growth in the economy in one year. Although possible, a 6.7% real growth in just one year is relatively rare in a modern, economy such as the U.S., Canada, Japan, or Western Europe. Normally, real growth rates are in the 2-5% range for such nations.
A final note about growth rates: It is possible using the above formula to calculate the percent growth over a longer period of time. For example, if we used real GDP for the year 1997 and for 2007, we could calculate the percent growth over ten years. Such a growth percentage covers the compounded growth over all those years and should not be compared to a single year growth rate.